19+ a single vector by itself is linearly dependent
Bp is a basis for H. If there are any non-zero solutions then the vectors are linearly dependent.

Advanced Time Series Analysis Of Generally Irregularly Spaced Signals Beyond The Oversimplified Methods Sciencedirect
A basis is spanning set that is as large as possible.
. A basis is a spanning set that is as large as possible. If H span b1 bp. A set consisting of a single vector v is linearly dependent if and only if v 0.
Therefore any set consisting of a single nonzero vector is linearly independent. The only way to get the zero vector is to multiply this lone vector by zero. The columns of an invertible.
The formal definition of linear independence A set of vectors is linearly independent if and only if the equation. Answer 1 of 35. CIf H spanb1.
This definition is indeed equivalent to. Okay its not equal to 0. C 1 v 1 c 2 v 2 c k v k 0 has only the trivial solution.
Given a set of vectors you can determine if they are. Therefore only a single zero vector is linearly dependent while any set consisting of a single. If the only solution is x 0 then they are linearly independent.
In some cases the linear. A single vector by itself is linearly dependent. 1 point Check the true statements below.
Terms in this set 11 A single vector by itself is linearly dependent False it would have to be the zero vector to be linearly dependent by itself If H Span b1bp then b1bp is a basis for. A set consisting of a single vector v is linearly dependent if and only if v 0. Then the given vectors are linearly independent.
A single vector by itself is linearly dependent. Then if if the determinant a 1 b 1 c 1 a 2 b 2 c 2 a 3 b 3 c 3 is not equal to 0 point. Math Vector space C.
A basis is a spanning set that is as large as possible. So let these be 3 vectors. When theres only one vector in the set this is obviously true.
The set containing the zero vector could be infinite and still be linearly dependent--the fact that the zero vector is in the set is enough for linear dependence all by itself. If H span b1 bp then b1 bp is a basis for H. Created by DrakeJa Terms in this set 41 A single vector by itself is linearly dependent.
False The columns of an invertible nxn. A single vector by itself is linearly dependent. False If H Span b1bp then b1bp is a basis for H.

Linear Independence Wikipedia

Microheterogeneity Of Topoisomerase Ia Ib And Their Dna Bound States Acs Omega

Linear Algebra Example Problems Linearly Independent Vectors 2 Youtube
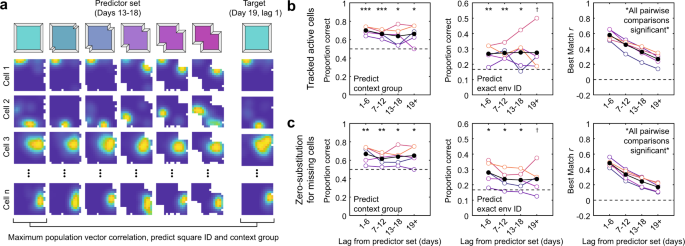
The Representation Of Context In Mouse Hippocampus Is Preserved Despite Neural Drift Nature Communications

Adult Education Budget Funding And Performance Management Rules 2022 To 2023 Gov Uk

Linearly Independent Vector An Overview Sciencedirect Topics
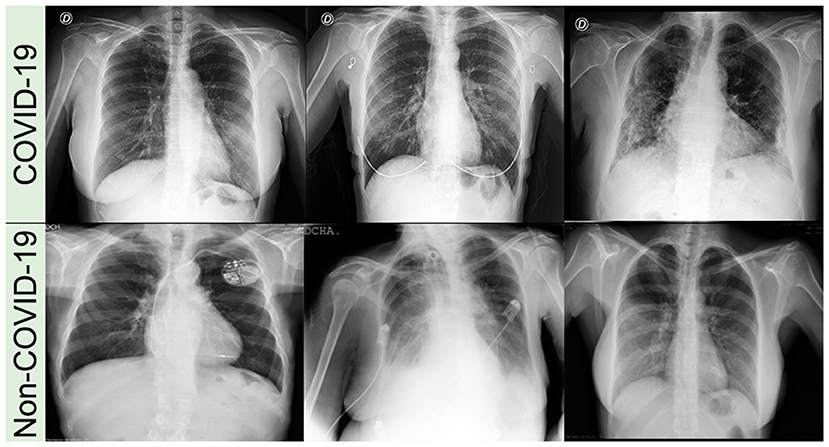
Frontiers Explainable Machine Learning For Covid 19 Pneumonia Classification With Texture Based Features Extraction In Chest Radiography

Adult Education Budget Funding And Performance Management Rules 2022 To 2023 Gov Uk

B Cell Overview Thermo Fisher Scientific Fr

Linear Independence And Linear Dependence Ex 1 Youtube
Full Article An Empirical Analysis Of Efficiency In The Indian Gold Futures Market
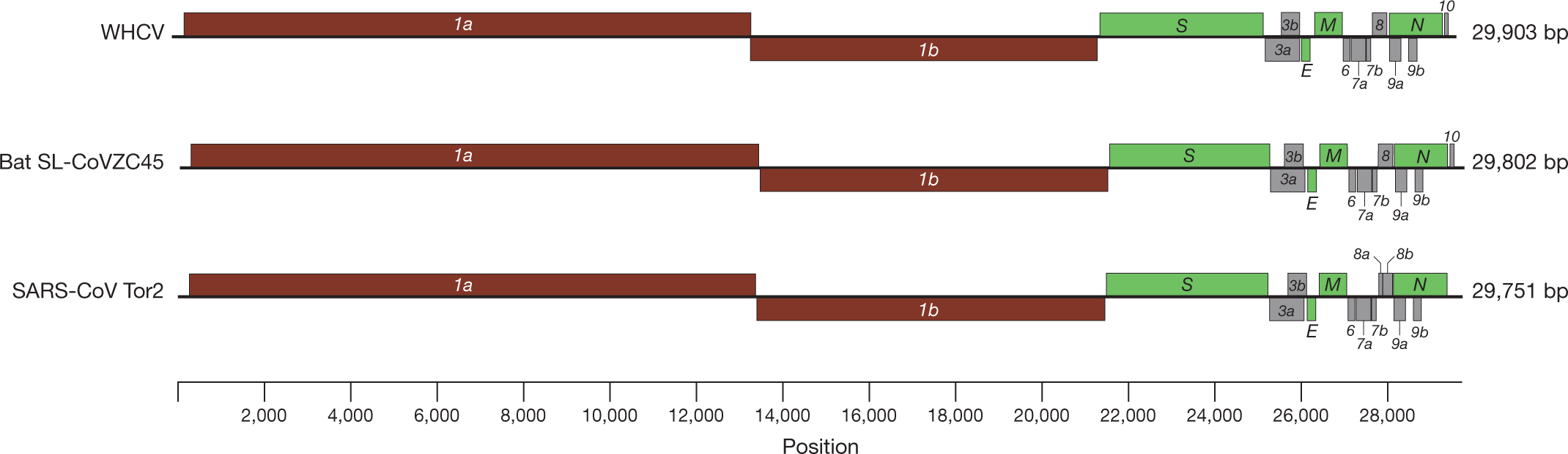
A New Coronavirus Associated With Human Respiratory Disease In China Nature
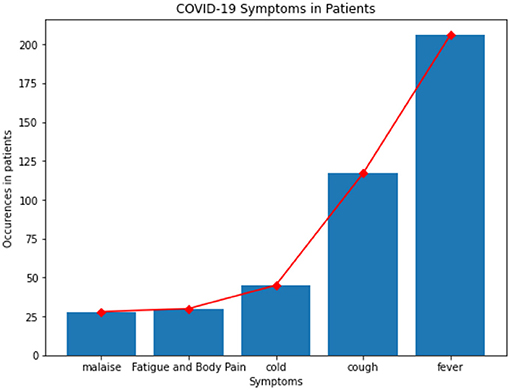
Frontiers Covid 19 Patient Health Prediction Using Boosted Random Forest Algorithm

Linear Independence Wikipedia

In Vivo Characterization Of Emerging Sars Cov 2 Variant Infectivity And Human Antibody Escape Potential Sciencedirect

Linearly Independent Vectors Definition Deepai
Estimating Covid 19 Cases In Makkah Region Of Saudi Arabia Space Time Arima Modeling Plos One